ByteDrift

Java图论库 Jgrapht

发表于 更新于 分类于
图(graph)是一种数据结构，是目前应用最广泛的数据结构，它能实现抽象的功能以及相当生活化的功能，应用范围包括计算机科学、语言学、物理和化学、社会科学、生物学和数学，包括目前热门的人工智能中的神经网络学习。

一 环境

由于Jgrapht是一个Java库，跨平台没有任何问题，环境方面无需赘述，一般的maven项目即可。

  • jdk16
  • maven 3.5.3

学习图论可以配合可视化的库一起学习更直观，所以我这里使用了一套开源的整合的可视化包 https://github.com/tomnelson/jungrapht-visualization （jgrapht-ext在顶点布局和友好度上不如这个库 ）

1
2
3
4
5
<dependency>
  <groupId>com.github.tomnelson</groupId>
  <artifactId>jungrapht-visualization</artifactId>
  <version>1.4</version>
</dependency>

这里面包含了 jgrapht-core:1.5.1 ，因此，如果你只需要核心功能，只需依赖：

1
2
3
4
5
<dependency>
    <groupId>org.jgrapht</groupId>
    <artifactId>jgrapht-core</artifactId>
    <version>${jgrapht.version}</version>
</dependency>

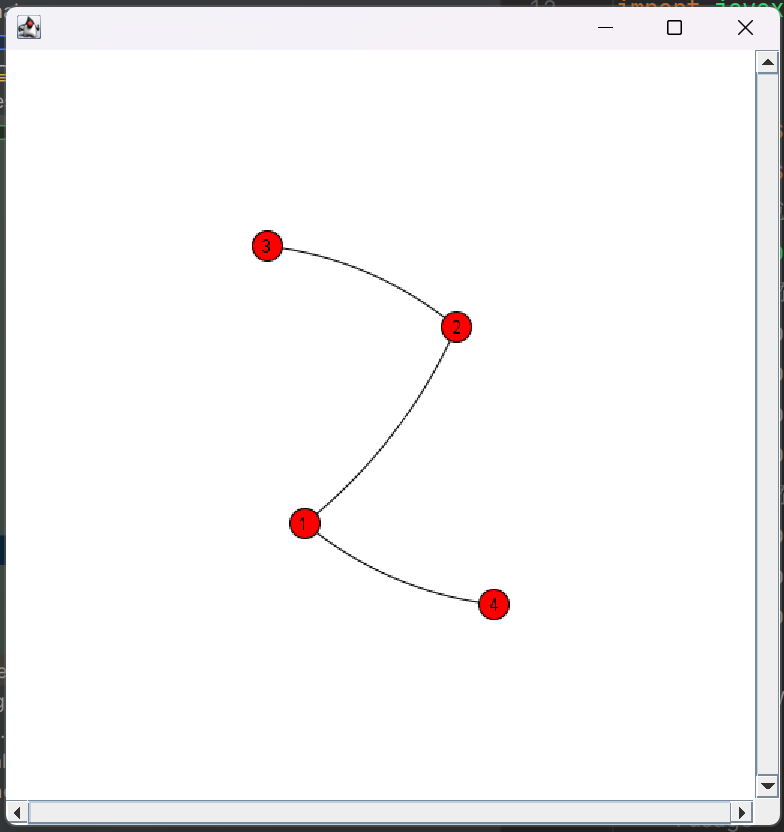
二 构建图

1. 无向图

1
2
3
4
5
6
7
8
9
10
11
12
// 创建图
SimpleGraph<Integer, DefaultEdge> graph = new SimpleGraph<>(DefaultEdge.class);
// 添加顶点
graph.addVertex(1);
graph.addVertex(2);
graph.addVertex(3);
graph.addVertex(4);
// 添加边
graph.addEdge(1, 2);
graph.addEdge(1, 4);
graph.addEdge(2, 3);

我们可以使用jungrapht-visualization展示这个图，添加如下方法：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
public static void showGraph(Graph<?, ?> g) {
     JFrame f = new JFrame();
     f.setLayout(new BorderLayout());
     Dimension size = new Dimension(1000, 1000);
     VisualizationModel<?, ?> vm =
             VisualizationModel.builder(g)
                     .layoutAlgorithm(new KKLayoutAlgorithm<>())
                     .layoutSize(size)
                     .build();
     final VisualizationViewer<?, ?> vv =
             VisualizationViewer
                     .builder(vm)
                     .viewSize(size)
                     .build();
     vv.getRenderContext().setVertexLabelFunction(Object::toString);
     vv.getRenderContext().setVertexLabelPosition(Renderer.VertexLabel.Position.CNTR);
     vv.setVertexToolTipFunction(Object::toString);
     VisualizationScrollPane visualizationScrollPane = new VisualizationScrollPane(vv);
     f.add(visualizationScrollPane);

     f.setDefaultCloseOperation(WindowConstants.EXIT_ON_CLOSE);
     f.pack();
     f.setVisible(true);
 }

将我们的graph传入

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
public static void main(String[] args) {
    // 创建图
    SimpleGraph<Integer, DefaultEdge> graph = new SimpleGraph<>(DefaultEdge.class);
    // 添加顶点
    graph.addVertex(1);
    graph.addVertex(2);
    graph.addVertex(3);
    graph.addVertex(4);
    // 添加边
    graph.addEdge(1, 2);
    graph.addEdge(1, 4);
    graph.addEdge(2, 3);

    showGraph(graph);
}

1

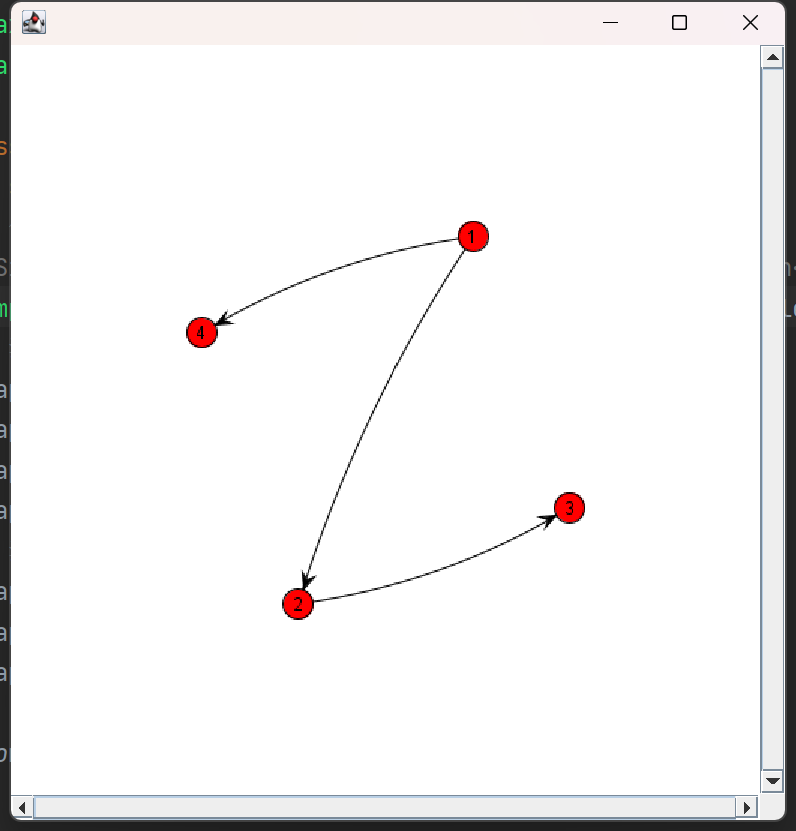
2. 有向图

同理可以构建有向图：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
    public static void main(String[] args) {
        // 创建图
//        SimpleGraph<Integer, DefaultEdge> graph = new SimpleGraph<>(DefaultEdge.class);
        SimpleDirectedGraph<Integer, DefaultEdge> graph = new SimpleDirectedGraph<>(DefaultEdge.class);
        // 添加顶点
        graph.addVertex(1);
        graph.addVertex(2);
        graph.addVertex(3);
        graph.addVertex(4);
        // 添加边
        graph.addEdge(1, 2);
        graph.addEdge(1, 4);
        graph.addEdge(2, 3);

        showGraph(graph);
    }

2

我们在上面的例子中使用Integer作为Vertex （顶点）的泛型。使用DefaultEdge 作为 Edge （边）的泛型。类似jdk里的各种数据结构，这里对于Vertex的泛型没有任何约束。

1
public interface Graph<V, E> {}

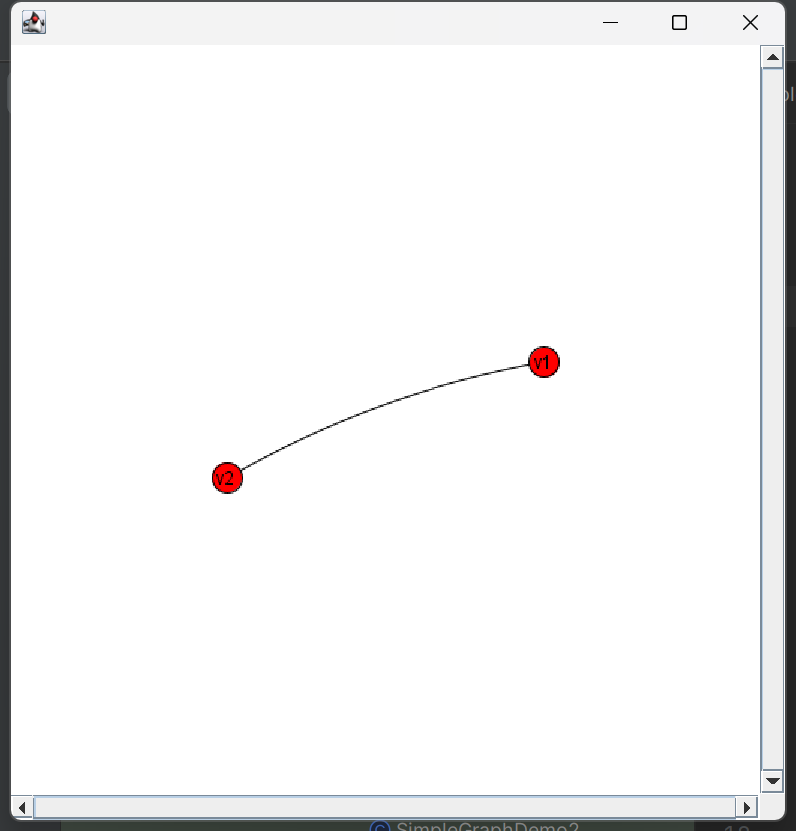
和Map同样的道理我们需要重写hashCode和equals来构建自己的Vertex

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
static class MyVertex {
    String name;

    public MyVertex(String name) {
        this.name = name;
    }

    @Override
    public int hashCode() {
        return name.hashCode();
    }

    @Override
    public boolean equals(Object obj) {
        return ((MyVertex) obj).name.equals(name);
    }

    @Override
    public String toString() {
        return name;
    }
}

public static void main(String[] args) {
    SimpleGraph<MyVertex, DefaultEdge> graph = new SimpleGraph<>(DefaultEdge.class);
    graph.addVertex(new MyVertex("v1"));
    graph.addVertex(new MyVertex("v2"));
    graph.addEdge(new MyVertex("v1"), new MyVertex("v2"));
    showGraph(graph);
}

需要记得重写toString ，否则可视化库将调用Object的toString方法渲染vertex标签。
3

此外，Edge也没有任何限制，但是有时用户会选择继承DefaultEdge 的原因是，在默认的Graph实现中，框架会自动识别Edge类型，如果是DefaultEdge的子类则会自动填充其 边两端的顶点

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
/**
 * A default implementation for edges in a {@link Graph}.
 *
 * @author Barak Naveh
 */
public class DefaultEdge
    extends
    IntrusiveEdge
{
    private static final long serialVersionUID = 3258408452177932855L;

    /**
     * Retrieves the source of this edge. This is protected, for use by subclasses only (e.g. for
     * implementing toString).
     *
     * @return source of this edge
     */
    protected Object getSource()
    {
        return source;
    }

    /**
     * Retrieves the target of this edge. This is protected, for use by subclasses only (e.g. for
     * implementing toString).
     *
     * @return target of this edge
     */
    protected Object getTarget()
    {
        return target;
    }

    @Override
    public String toString()
    {
        return "(" + source + " : " + target + ")";
    }
}

需要注意注释所说，这里source和target都是protected，只能在子类中访问，外部访问需要在子类暴露一个函数。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
    static class Dummy extends DefaultEdge {
        public Integer getSrc() {
            return (Integer) getSource();
        }

        public Integer getTarget0() {
            return (Integer) getTarget();
        }
    }

    public static void main(String[] args) {
        // 创建图
//        SimpleGraph<Integer, DefaultEdge> graph = new SimpleGraph<>(DefaultEdge.class);
        SimpleDirectedGraph<Integer, Dummy> graph = new SimpleDirectedGraph<>(Dummy.class);
        // 添加顶点
        graph.addVertex(1);
        graph.addVertex(2);
        graph.addVertex(3);
        graph.addVertex(4);
        // 添加边
        graph.addEdge(1, 2);
        graph.addEdge(1, 4);
        graph.addEdge(2, 3);

        for (Dummy dummy : graph.edgeSet()) {
            System.out.println(dummy.getSrc() + " " + dummy.getTarget0());
        }
    }
1 2
1 4
2 3

3. 有权图

有权图怎么构建呢？

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

public static void main(String[] args) {
    Graph<Integer, DefaultWeightedEdge> g = new DefaultUndirectedWeightedGraph<>(DefaultWeightedEdge.class);

    g.addVertex(1);
    g.addVertex(2);
    g.addVertex(3);
    g.addVertex(4);

    DefaultWeightedEdge defaultWeightedEdge = g.addEdge(1, 2);
    g.setEdgeWeight(defaultWeightedEdge,1);
    DefaultWeightedEdge defaultWeightedEdge1 = g.addEdge(2, 3);
    g.setEdgeWeight(defaultWeightedEdge1,2);
    DefaultWeightedEdge defaultWeightedEdge2 = g.addEdge(1, 3);
    g.setEdgeWeight(defaultWeightedEdge2,3);

    showGraph(g);
}

4. 子图

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
    public static void main(String[] args) {
        // 创建图
//        SimpleGraph<Integer, DefaultEdge> graph = new SimpleGraph<>(DefaultEdge.class);
        SimpleDirectedGraph<Integer, DefaultEdge> graph = new SimpleDirectedGraph<>(DefaultEdge.class);
        // 添加节点
        for (int i = 0; i < 10; i++) {
            graph.addVertex(i);
        }

        // 添加边
        DefaultEdge e1 = graph.addEdge(1, 2);
        DefaultEdge e2 = graph.addEdge(1, 4);
        DefaultEdge e3 = graph.addEdge(2, 3);
        DefaultEdge e4 = graph.addEdge(2, 5);

        AsSubgraph<Integer, DefaultEdge> sub = new AsSubgraph<>(graph, Set.of(3, 4, 5), Set.of(e1, e3));

        BreadthFirstIterator<Integer, DefaultEdge> iter = new BreadthFirstIterator<>(sub);
        while (iter.hasNext()) {
            System.out.println(iter.next());
        }
        showGraph(graph);
    }

三 图算法

1. 遍历

如何遍历呢？比较常用的有：广度优先遍历，深度优先遍历，拓扑遍历，广度优先遍历和深度优先遍历具体原理这里不再详述。

需要注意的是：深度优先和广度优先可用于无向或有向图，拓扑遍历只能用于有向无环图（DAG）。在图论中，我们经常讨论有向无环图DAG（Directed Acyclic Graph），这类图常用来描述顶点之间的依赖关系（先修课程、软件包的安装依赖）。对于DAG，我们可以对其进行拓扑排序。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
    public static void main(String[] args) {
        // 创建图
        SimpleGraph<Integer, DefaultEdge> graph = new SimpleGraph<>(DefaultEdge.class);
//        SimpleDirectedGraph<Integer, DefaultEdge> graph = new SimpleDirectedGraph<>(DefaultEdge.class);
        // 添加顶点
        graph.addVertex(1);
        graph.addVertex(2);
        graph.addVertex(3);
        graph.addVertex(4);
        graph.addVertex(5);
        graph.addVertex(6);
        // 添加边
        graph.addEdge(1, 2);
        graph.addEdge(1, 4);
        graph.addEdge(2, 3);
        graph.addEdge(1, 5);
        graph.addEdge(2, 6);
        // 广度优先遍历
        BreadthFirstIterator<Integer, DefaultEdge> iter = new BreadthFirstIterator<>(graph);
        // 深度优先遍历
//        DepthFirstIterator<Integer, DefaultEdge> iter = new DepthFirstIterator<>(graph);
        // 拓扑遍历
//        TopologicalOrderIterator<Integer, DefaultEdge> iter = new TopologicalOrderIterator<>(graph);
        while (iter.hasNext()) {
            System.out.println(iter.next());
        }
        showGraph(graph);
    }

2. 最短路径

最短路径算法较多，如广度优先搜索（深度优先无法得到最短路径），A*算法 ，Dijkstra算法，Floyd等，以上算法还有诸多变种。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
    public static void main(String[] args) {
        // 创建图
        SimpleGraph<Integer, DefaultEdge> graph = new SimpleGraph<>(DefaultEdge.class);
//        SimpleDirectedGraph<Integer, DefaultEdge> graph = new SimpleDirectedGraph<>(DefaultEdge.class);
        // 添加节点
        graph.addVertex(1);
        graph.addVertex(2);
        graph.addVertex(3);
        graph.addVertex(4);
        graph.addVertex(5);
        graph.addVertex(6);
        graph.addVertex(7);
        // 添加边
        graph.addEdge(1, 2);
        graph.addEdge(1, 4);
        graph.addEdge(2, 3);
        graph.addEdge(1, 5);
        graph.addEdge(2, 6);

        ShortestPathAlgorithm<Integer, DefaultEdge> shortPathAlg = new DijkstraShortestPath<>(graph);
//        ShortestPathAlgorithm<Integer, DefaultEdge> shortPathAlg = new FloydWarshallShortestPaths<>(graph);
//        ShortestPathAlgorithm<Integer, DefaultEdge> shortPathAlg = new BFSShortestPath<>(graph);
//        ShortestPathAlgorithm<Integer, DefaultEdge> shortPathAlg = new AStarShortestPath<>(graph, new ALTAdmissibleHeuristic<>(graph, new HashSet<>()));
        GraphPath<Integer, DefaultEdge> path = shortPathAlg.getPath(1, 6);
        for (DefaultEdge defaultEdge : path.getEdgeList()) {
            System.out.println(defaultEdge);
        }
        showGraph(graph);
    }

由于我们的样例图不存在权重，所以使用BFS和Dijkstra效果是一样的。Dijkstra（迪杰斯特拉）算法是典型的单源最短路径算法，用于计算某个顶点到其他所有顶点的最短路径。Dijkstra（迪杰斯特拉）算法要求图中不存在负权边，即保证图中每条边的权重值为正。算法的基本思想是：从源点出发，每次选择离源点最近的一个顶点前进，然后以该顶点为中心进行扩展，最终得到源点到其余所有点的最短路径。

上面的最短路径算法中A*算法需要配置启发函数。其他的只需将图传入即可。

3. 连通性检测

connectedSets api可以将图划分为多个联通子图

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
    public static void main(String[] args) {
        // 创建图
//        SimpleGraph<Integer, DefaultEdge> graph = new SimpleGraph<>(DefaultEdge.class);
        SimpleDirectedGraph<Integer, DefaultEdge> graph = new SimpleDirectedGraph<>(DefaultEdge.class);
        // 添加节点
        graph.addVertex(1);
        graph.addVertex(2);
        graph.addVertex(3);
        graph.addVertex(4);
        // 添加边
        graph.addEdge(1, 2);
        graph.addEdge(2, 3);

        ConnectivityInspector<Integer, DefaultEdge> inspector = new ConnectivityInspector<>(graph);
        List<Set<Integer>> sets = inspector.connectedSets();
        for (Set<Integer> s : sets) {
            System.out.println(s);
        }
    }

[1, 2, 3]
[4]

判断图是否联通

1
2
3
4
5
public static void main(String[] args) {
    ...
    ConnectivityInspector<Integer, DefaultEdge> inspector = new ConnectivityInspector<>(graph);
    System.out.println(inspector.isConnected());
}

这个算法的本质就是查看分组的联通子图是否为1，和前一个api是一套实现。

判断两个顶点是否连通

1
2
3
4
5
public static void main(String[] args) {
    ...
    ConnectivityInspector<Integer, DefaultEdge> inspector = new ConnectivityInspector<>(graph);
    boolean b = inspector.pathExists(1, 4);
}

强连通：强连通首先只用于有向图，强连通意味着如果我们从当前顶点开始遍历，可以达到任意顶点。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
    public void setup() {
//        g = new SimpleGraph<>(null, new IdEdgeFactory(), false);
        g = new SimpleDirectedGraph<>(null, new IdEdgeFactory(), false);
        for (int i = 0; i < 20; i++) {
            g.addVertex(i);
        }

        g.addEdge(1, 3);
        g.addEdge(3, 1);
        g.addEdge(1, 2);
        g.addEdge(2, 3);
        g.addEdge(4, 3);
        g.addEdge(7, 8);
        g.addEdge(8, 1);
        g.addEdge(8, 1);
        g.addEdge(8, 10);


        StrongConnectivityAlgorithm<Integer, IdEdge> scAlg
                = new KosarajuStrongConnectivityInspector<>(g);
        for (Set<Integer> integers : scAlg.stronglyConnectedSets()) {
            System.out.println(integers);
        }

        List<Graph<Integer, IdEdge>> stronglyConnectedComponents = scAlg.getStronglyConnectedComponents();
        for (Graph<Integer, IdEdge> stronglyConnectedComponent : stronglyConnectedComponents) {
            System.out.println(stronglyConnectedComponent);
        }

        System.out.println(scAlg.isStronglyConnected());
    }

4. 欧拉回路

与著名的七桥问题，和一笔画问题的概念相关。

欧拉路径

如果图G中的一个路径包括每个边恰好一次，则该路径称为欧拉路径(Euler path)。

欧拉回路

如果一个回路是欧拉路径，则称为欧拉回路(Euler circuit)。

是否存在欧拉回路的判断：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
g = new SimpleDirectedGraph<>(null, new IdEdgeFactory(), false);
g.addVertex(1);
g.addVertex(2);
g.addVertex(3);
g.addVertex(4);

g.addEdge(1, 2);
g.addEdge(2, 3);
g.addEdge(3, 4);
g.addEdge(4, 1);

HierholzerEulerianCycle eulerianCycle
        = new HierholzerEulerianCycle<>();
GraphPath eulerianCycle1 = eulerianCycle.getEulerianCycle(g);

5. 环检测

jgrapht环检测算法也较多，这里不再一一列举

1
2
3
4
5
6
7
8
9
10
11
12
13
14
g = new SimpleDirectedGraph<>(null, new IdEdgeFactory(), false);
g.addVertex(1);
g.addVertex(2);
g.addVertex(3);
g.addVertex(4);

g.addEdge(1, 2);
g.addEdge(2, 3);
g.addEdge(3, 4);
g.addEdge(4, 1);
CycleDetector<Integer, IdEdge> cycleDetector
        = new CycleDetector<>(g);

System.out.println(cycleDetector.detectCycles());

6. 最小生成树

图中边的权值最小的生成树，这里的两个著名算法Prim和Kruskal

1
2
3
4
5
6
7
...
        SpanningTreeAlgorithm<IdEdge> spanningTreeAlgorithm = new PrimMinimumSpanningTree<>(g);
        for (IdEdge idEdge : spanningTreeAlgorithm.getSpanningTree()) {
            System.out.println(idEdge);
        }


本人对图论了解不深，所以目前只学习到了这些较为常用的API。后续有新的好用的API会继续更新。

  • 本文作者： fenix
  • 本文链接： https://fenix0.com/jgrapht/
  • 版权声明： 本博客所有文章除特别声明外，均采用 BY-NC 许可协议。转载请注明出处！