跳跃问题是即典型的贪心类问题，贪心算法可以在动态规划的基础上进一步降低时间复杂度。

特征

通常为，你有一个数组，数组中保存的值是每个slot上可以跳的最大距离。

55. 跳跃游戏

给定一个非负整数数组 nums ，你最初位于数组的第一个下标。

数组中的每个元素代表你在该位置可以跳跃的最大长度。

判断你是否能够到达最后一个下标。

boolean canJump(int[] nums) {
    int n = nums.length;
    int max = 0;
    for (int i = 0; i < n - 1; i++) {
        max = Math.max(max, i + nums[i]);
        if (max <= i) {
            return false;
        }
    }
    return max >= n - 1;
}

这里尝试计算每个节点能到达的最远距离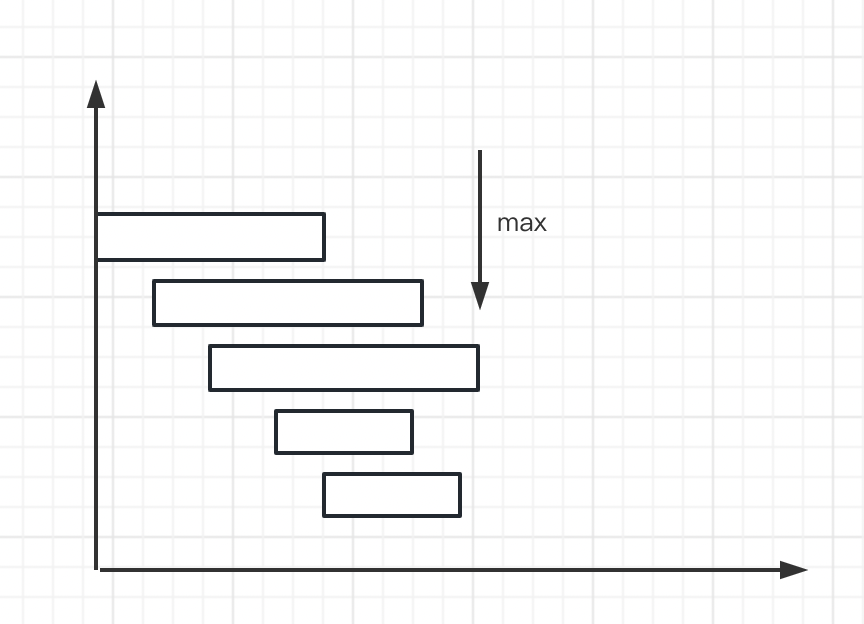

并更新其最值，直到发现最值不能满足当前遍历进度。说明不能满足跳跃需求了，由于目标是最后一个点，所以n-1不用遍历。

45. 跳跃游戏 II

给定一个长度为 n 的 0 索引整数数组 nums。初始位置为 nums[0]。

每个元素 nums[i] 表示从索引 i 向前跳转的最大长度。换句话说，如果你在 nums[i] 处，你可以跳转到任意 nums[i + j] 处:

0 <= j <= nums[i]
i + j < n
返回到达 nums[n - 1] 的最小跳跃次数。生成的测试用例可以到达 nums[n - 1]。

int jump(int[] nums) {
    int end = 0, max = 0;
    int jumps = 0;
    for (int i = 0; i < nums.length - 1; i++) {
        max = Math.max(nums[i] + i, max);
        if (end == i) {
            jumps++;
            end = max;
        }
    }
    return jumps;
}

还是和前面一样的推进最值，每次遍历到边界就用当前的最大值扩展边界。最终扩展的次数就是最小的次数。