单调栈的一些应用

概念

什么是单调栈呢？

• 单调栈首先是栈，即，这是个能存储数据的数据结构并满足后进先出的特性。
• 其次单调栈要满足单调的特性，及栈中的元素是有序的，要么栈顶到栈底从小到大，要么从大到小。

单调栈有啥用？

应该说单调栈的应用并不是非常广泛，只能用于解决一类特定问题：一组数据中，为每个元素找出左边（右边）比它大（小）的第一个元素。

比如我们现在有一个数组需要找出每个元素右边比他大的第一个元素。如果暴力求解扫描每个元素后面的最值，将带来 O(n^2) 复杂度。如果使用单调栈法则有O(n)复杂度。

单调栈的解法：

int[] monoStack(int[] nums) {
    int n = nums.length;
    // 用于保存结果
    int[] res = new int[n];
    // 单调栈本体
    Deque<Integer> s = new ArrayDeque<>();
    // 由于我们要的是右边的最大值，需要 反向循环
    for (int i = n - 1; i >= 0; i--) {
        // 只要当前元素比栈顶元素大，则不停弹出栈顶元素
        while (!s.isEmpty() && s.peek() <= nums[i]) s.pop();
        // 此时栈顶元素 要么比当前元素大，要么栈上已经没有元素
        res[i] = s.isEmpty() ? -1 : s.peek();
        // 当前元素入栈，此时当前元素是栈中最小的
        // 栈中数据仍是递增的
        s.push(nums[i]);
    }
    return res;
}

应该如何理解上面的逻辑？无论

while (!s.isEmpty() && s.peek() <= nums[i]) s.pop(); 和 es[i] = s.isEmpty() ? -1 : s.peek();

如何执行，也不影响最后每个元素都会入栈。最终每个元素都被 push 入栈了一次，而最多会被 pop 一次，没有任何冗余操作。所以这里复杂度是 O(n)。

其次，while (!s.isEmpty() && s.peek() <= nums[i]) s.pop(); 这行意味着新元素总是挤出比自己小的元素，确保自己是最小的。当再也无法弹出后，栈顶元素是次小的（相对于当前元素），则此元素是我们要的右边比他大的第一个元素 。 我们可以将其保存起来。

例题1 求最大图形面积

leetcode 84
https://leetcode.cn/problems/largest-rectangle-in-histogram

给定 n 个非负整数，用来表示柱状图中各个柱子的高度。每个柱子彼此相邻，且宽度为 1 。
求在该柱状图中，能够勾勒出来的矩形的最大面积。

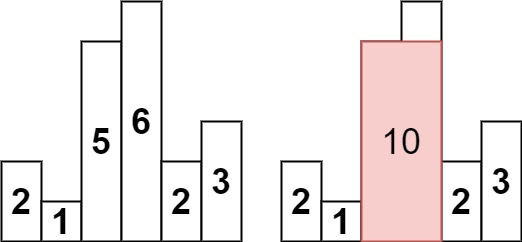
当临近的柱子比当前的柱子高的时候，矩形可以扩展，此时矩阵的高就是当前的柱子的高，矩阵的宽就是两边第一次遇到小于当前柱子高的距离，加到一起就是矩阵整体的宽的。宽高一乘就是面积了。

所以这里有两种解法，一种是左边求一遍单调栈，右边求一遍单调栈

public int largestRectangleArea(int[] heights) {
    Deque<Integer> d = new ArrayDeque<>();
    int ret = 0;
     // left[i]含义：i处右边最近的比heights[i]小的索引
    int[] left = new int[heights.length];
     // right[i]含义：i处左边最近的比heights[i]小的索引
    int[] right = new int[heights.length];
    for (int i = 0; i < heights.length; i++) {
        while (!d.isEmpty() && heights[d.peek()] >= heights[i]) d.poll();
        left[i] = d.isEmpty() ? -1 : d.peek();
        d.push(i);
    }

    d.clear();
    for (int i = heights.length - 1; i >= 0; i--) {
        while (!d.isEmpty() && heights[d.peek()] >= heights[i]) d.poll();
        right[i] = d.isEmpty() ? heights.length : d.peek();
        d.push(i);
    }

    for (int i = 0; i < left.length; i++) {
        ret = Math.max(ret, (right[i] - left[i] - 1) * heights[i]);
    }
    return ret;
}

另一种则是一次遍历的方案，这里注意的是，首先因为要计算宽度，所以这里栈中保存的是索引。其次每次弹出元素和每次需要入栈是另一种逆操作。最重要的是这里能一次找出两边的次小值的原因是，每次弹出的元素对应的右次小值可以求出，同时pop完成后最终入栈的又是左次小值。

public int largestRectangleArea(int[] heights) {
    int n = heights.length;
    int[] left = new int[n];
    int[] right = new int[n];
    Arrays.fill(right, n);
    Deque<Integer> d = new ArrayDeque<>();
    for (int i = 0; i < n; i++) {
        while (!d.isEmpty() && heights[d.peek()] > heights[i]) right[d.poll()] = i;
        left[i] = d.isEmpty() ? -1 : d.peek();
        d.push(i);
    }
    int ans = 0;
    for (int i = 0; i < n; ++i) {
        ans = Math.max(ans, (right[i] - left[i] - 1) * heights[i]);
    }
    return ans;
}

例题2 接雨水

非常经典的题了。

给定 n 个非负整数表示每个宽度为 1 的柱子的高度图，计算按此排列的柱子，下雨之后能接多少雨水。
示例 1：

public int trap(int[] height) {
    int n = height.length;
    int ans = 0;
    Deque<Integer> d = new ArrayDeque<>();
    for (int i = 0; i < n; i++) {
        while (!d.isEmpty() && height[d.peek()] < height[i]) {
            Integer cur = d.poll();
            if (d.isEmpty()) break;
            int l = d.peek();
            int r = i;
            int h = Math.min(height[r], height[l]) - height[cur];
            ans += (r - l - 1) * h;
        }
    }
    return ans;

}