学习python数据分析 三 numpy（2）

相关性

多项式

poly1d是NumPy中的一个类，用于表示一元多次多项式，即一个多项式只有一个自变量。poly1d的主要作用是方便用户对多项式进行各种运算，如加、减、乘、除、取幂、求导数和积分等。
在使用poly1d时，用户可以将一组多项式系数作为参数传入，例如：

import numpy as np

# 创建一个一元二次多项式 p(x) = 2x^2 + 3x + 4
p = np.poly1d([2, 3, 4])

创建完多项式后，用户可以对多项式进行各种运算。例如：

# 求多项式的值
print(p(1))  # 输出：9

# 求多项式的导数
p_deriv = p.deriv()
print(p_deriv)  # 输出：Poly1d([4, 3], dtype=int32)

除了使用系数来创建多项式之外，还可以使用多项式的根来创建多项式。例如：

# 创建一个一元三次多项式 p(x) = (x-1)(x-2)(x-3) = x^3 - 6x^2 + 11x - 6
p = np.poly1d([1, -6, 11, -6])

这里的多项式系数是通过多项式的根来计算得到的。

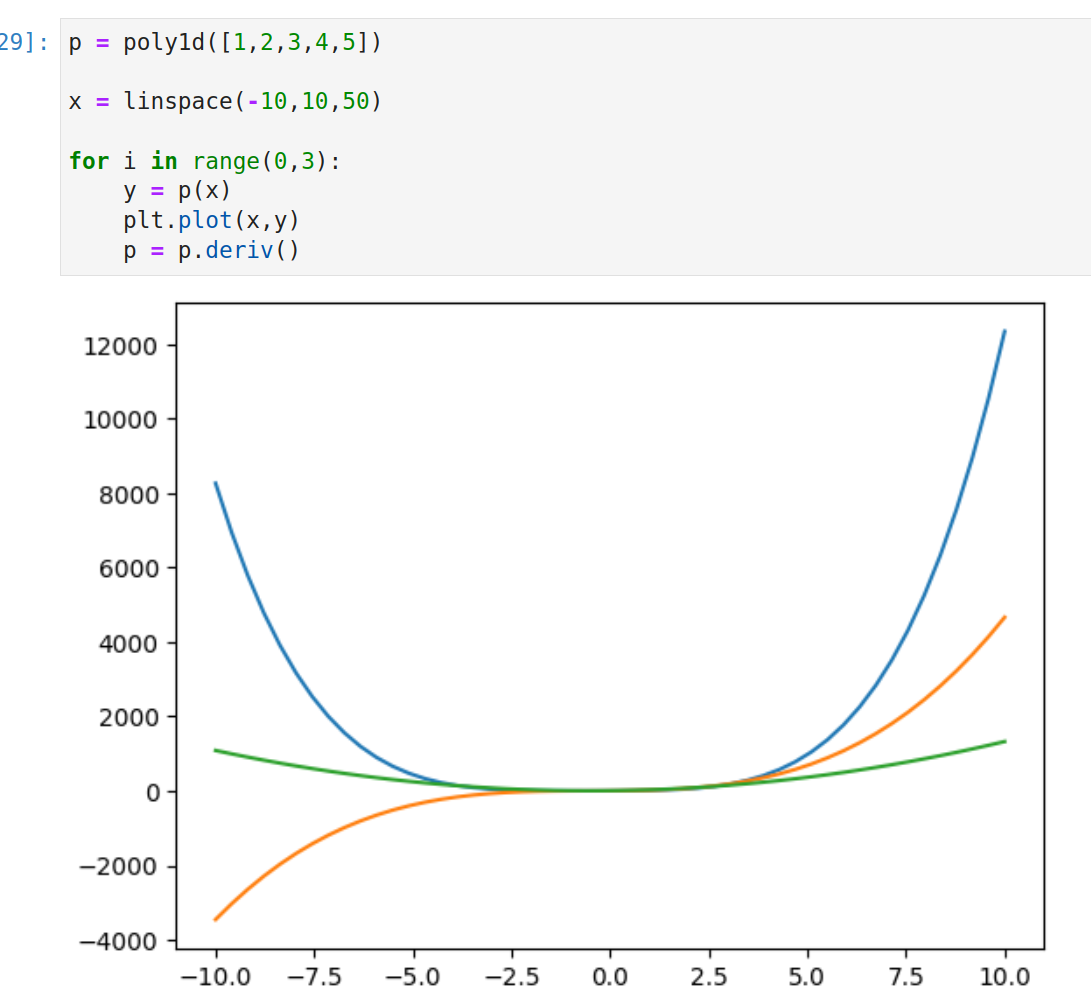
求导的一个演示
这里我们将poly1d转为了五元四次方程（多项式）
x ^ 4 + x^3 * 2+ x^2 * 3 + x * 4 + 5

其中每循环一次就求导并绘制

p = poly1d([1,2,3,4,5])

x = linspace(-10,10,50)

for i in range(0,3):
    y = p(x)
    plt.plot(x,y)
    p = p.deriv()

多项式拟合

多项式拟合本质上是numpy.polyfit是一个函数，用于拟合一系列数据点的多项式系数。它使用最小二乘法来拟合数据，将数据拟合为给定次数的多项式形式。

具体来说，numpy.polyfit(x, y, deg, rcond=None, full=False, cov=False)函数接受以下参数：

• x：一维数组，表示数据点的x坐标。
• y：一维数组，表示数据点的y坐标。
• deg：整数，表示拟合多项式的次数。
• rcond：可选参数，浮点数。控制奇异值在拟合过程中的影响。
• full：可选参数，布尔值。如果为True，则返回完整输出，包括残差、排名、奇异值以及拟合系数的协方差矩阵。
• cov：可选参数，布尔值。如果为True，则返回拟合系数的协方差矩阵。
  该函数返回一个一维数组，表示拟合多项式的系数。可以使用numpy.polyval函数将该系数用于计算多项式的值。

from numpy import *
import matplotlib.pyplot as plt
import datetime
def parse_price(price):
    return float(price[1:])

def parse_date(s):
    return datetime.datetime.strptime(s.decode('ascii'),"%m/%d/%Y").date().weekday()
all = genfromtxt('jd_all.csv',delimiter=',',skip_header=1,names=True,converters={3:parse_price,4:parse_price,5:parse_price,0:parse_date},usecols=(5)).astype('float')[0:100]

加载了京东的股价前100个点。

a=linspace(0,100,100)
# 拟合
fit = polyfit(a,all,10)
y2 = poly1d(fit)(a) 
# 画出原股价和拟合曲线
plt.plot(a,y2)
plt.plot(a,all)

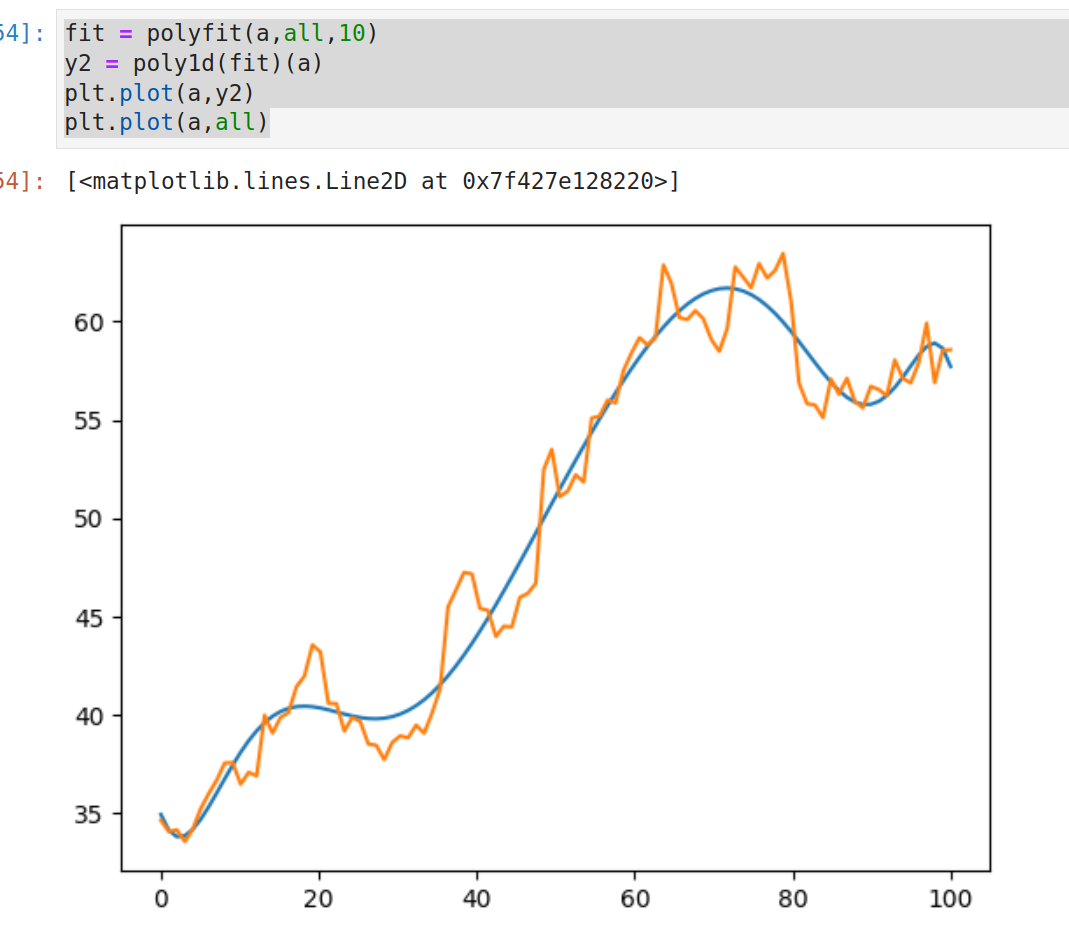
这里的10是拟合次数，拟合次数多了后，蓝色曲线就会过拟合。这里将其调整为50后，甚至会报出警告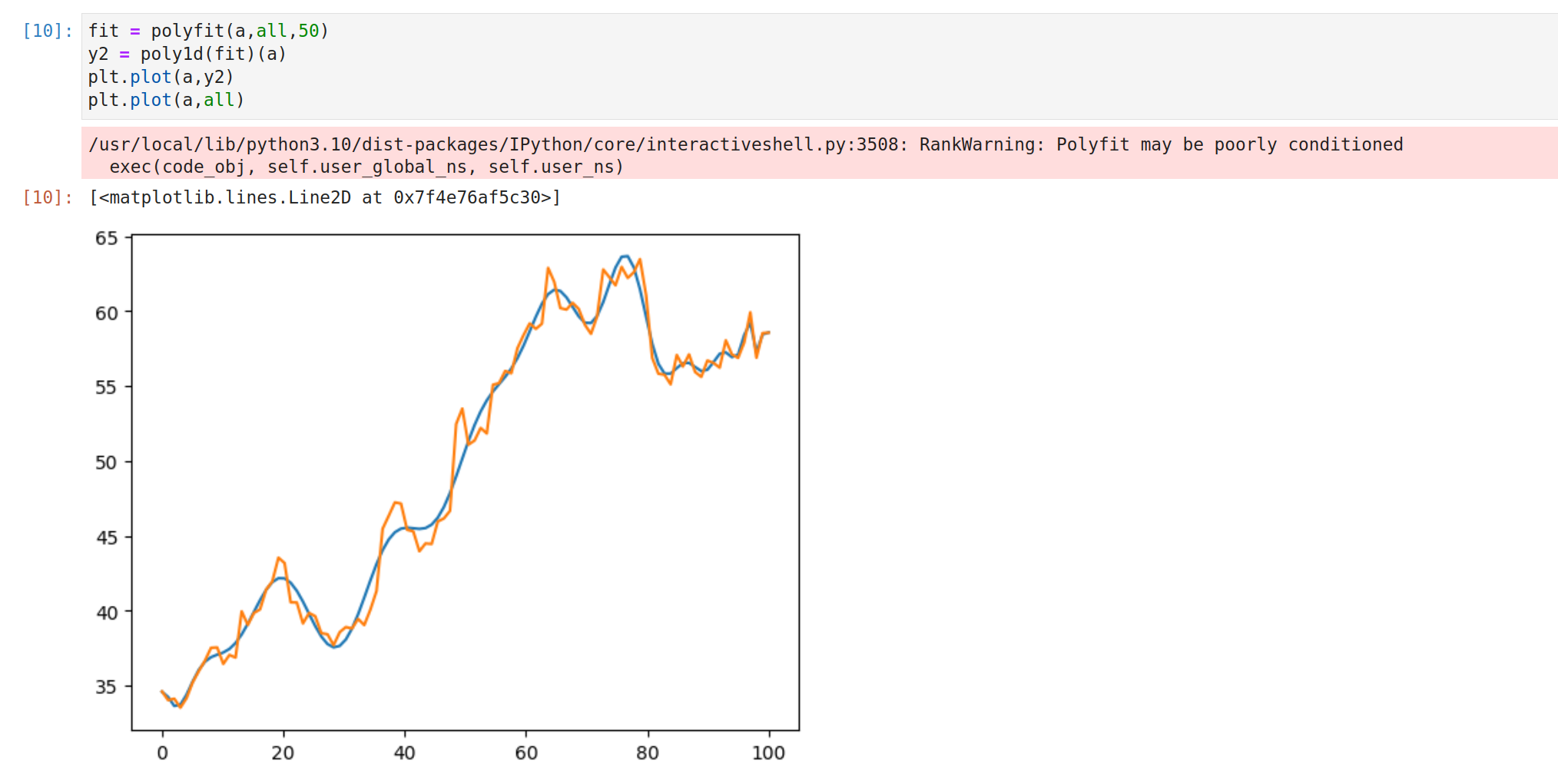

相关系数

这里我选了同济科技600846，上海临港600848某段时间内的开票价格。

import matplotlib.pyplot as plt
import numpy

p1 = numpy.load('600846.npy')[0:600]
p2 = numpy.load('600848.npy')[0:600]
x=numpy.linspace(0,1000,600)
plt.plot(x,p1)
plt.plot(x,p2)

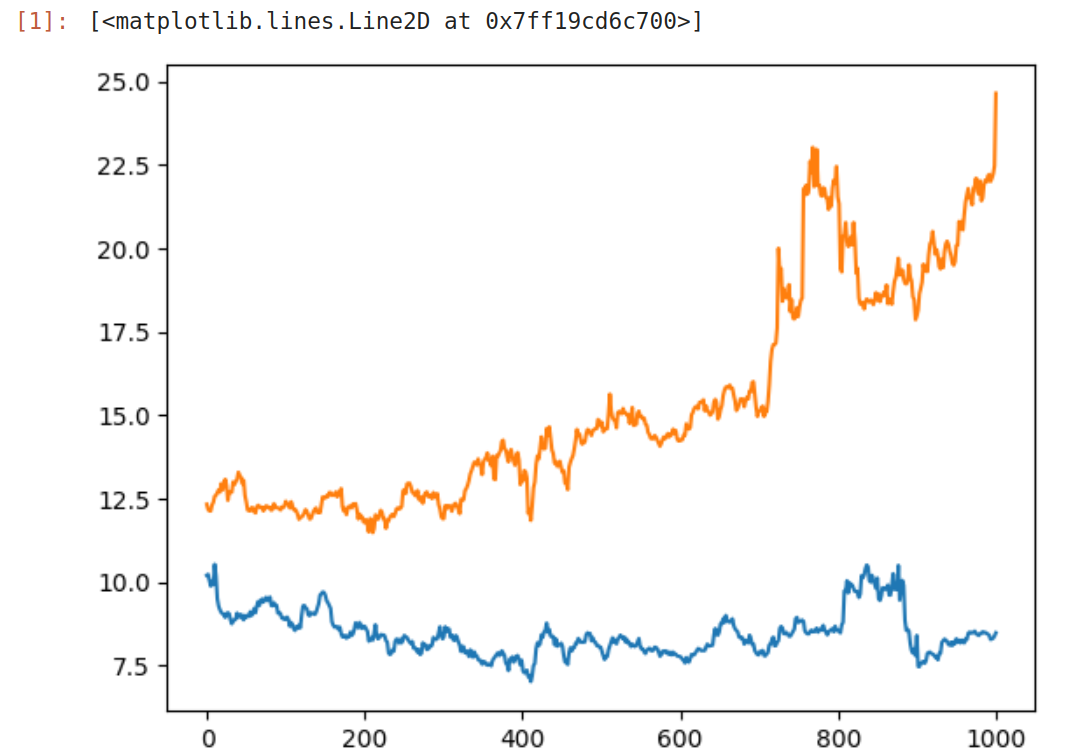
numpy.corrcoef(p1,p2)

array([[1.        , 0.11821975],
       [0.11821975, 1.        ]])

0.118

改为建设银行601939，工商银行601398后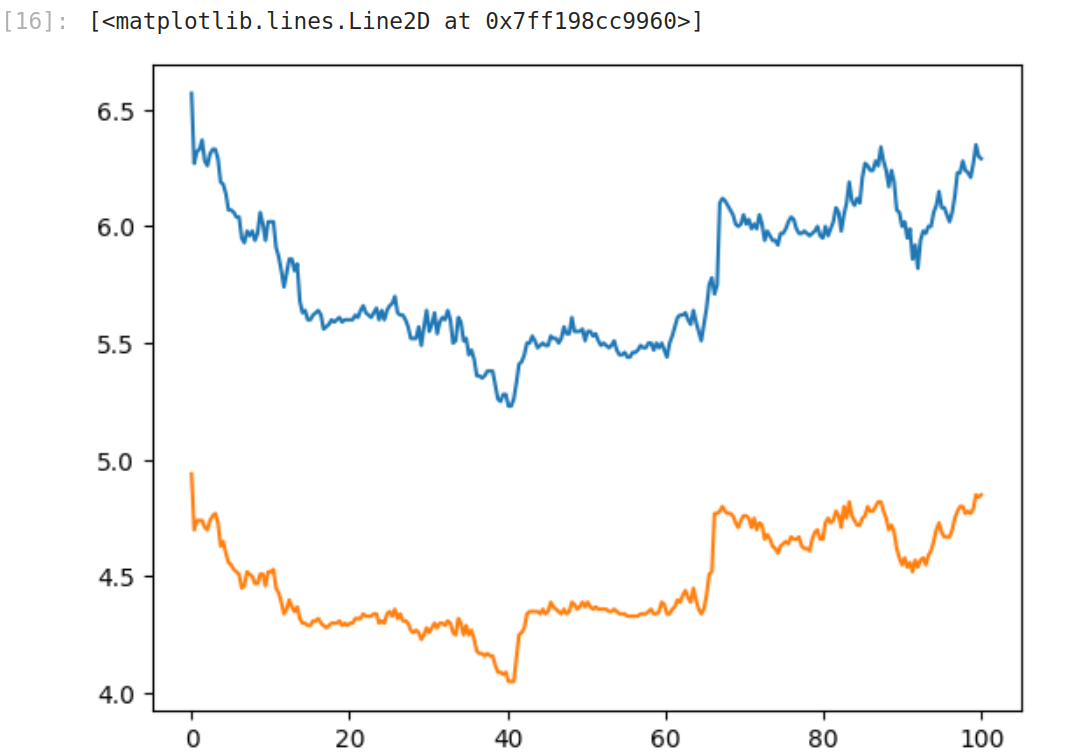

相关系数为 0.93021558，非常立竿见影。

汉宁窗口

w =numpy.hanning(N)
p4=numpy.convolve(w/w.sum(),p1)[N-1:-N+1]
plt.plot(x[N-1:],p1[N-1:])
plt.plot(x[N-1:],p4)

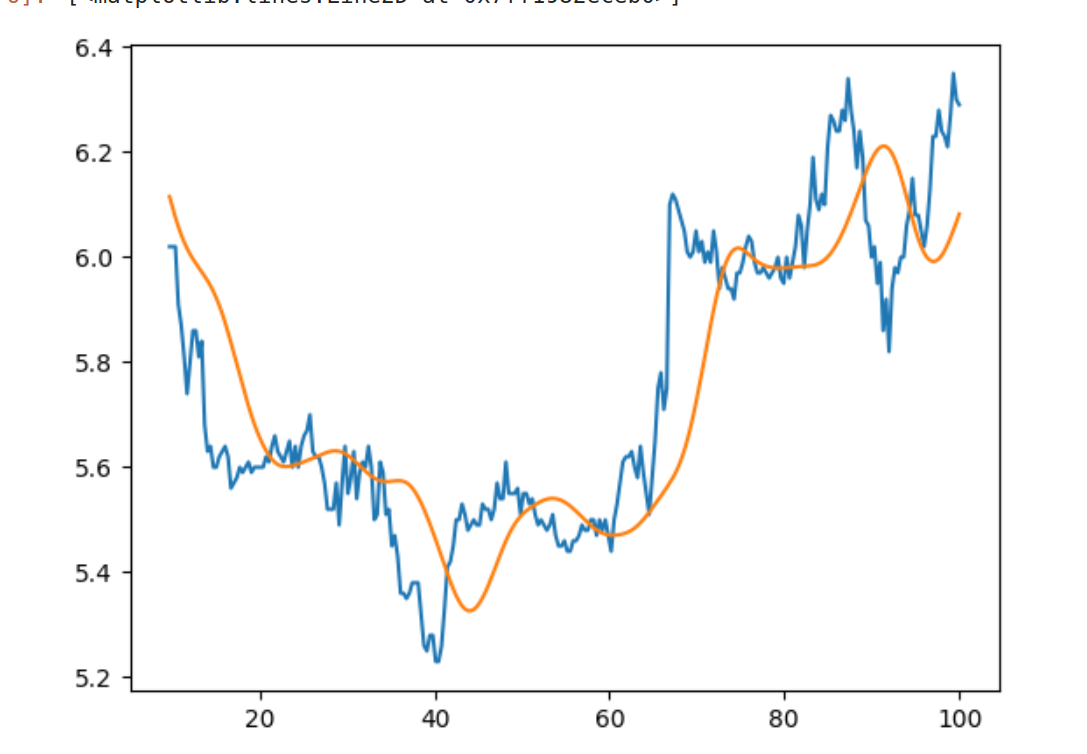
通常我们应该在使用这种方法降噪后，后再尝试拟合。