Rust与simd

什么是SIMD？

SIMD（Single Instruction Multiple Data）指令集，指单指令多数据流技术，可用一组指令对多组数据通进行并行操作。SIMD指令可以在一个控制器上控制同时多个平行的处理微元，一次指令运算执行多个数据流，这样在很多时候可以提高程序的运算速度。SIMD指令在本质上非常类似一个向量处理器，可对控制器上的一组数据（又称“数据向量”） 同时分别执行相同的操作从而实现空间上的并行。

什么处理器支持SIMD指令？

simd并不是某一个具体的指令，而是类似一个统称，只要满足单指令处理多组数据就可以成为simd指令。

MMX

MMX是由英特尔开发的一种SIMD多媒体指令集，共有57条指令。它于1996年集成在英特尔奔腾（Pentium）MMX处理器上，以提高其多媒体数据的处理能力。MMX指令集的向量寄存器是64bit。

SSE

SSE（英语：Streaming SIMD Extensions）是英特尔在AMD的3D Now!发布一年之后，在其计算机芯片Pentium III中引入的指令集，是继MMX的扩展指令集。SSE指令集提供了70条新指令。AMD后来在Athlon XP中加入了对这个新指令集的支持。
由于SSE加入了浮点支持，SSE就比MMX更加常用。而SSE2加入了整数运算支持之后让SSE更加的有弹性，当MMX变成是多余的指令集，SSE指令集甚至可以与MMX并发运作，在某些时候可以提供额外的性能增进。所有的SSE系列指令的向量寄存器都是128bit。

AVX

AVX指令集是Sandy Bridge和Larrabee架构下的新指令集，AVX是在之前的SSE128位扩展到和256位的单指令多数据流。

AVX出现在2008年，由128bit拓展到256bit，增强了数据重排和灵活的不对齐地址访问；
AVX2出现在2011年，增加了256bit的整数向量操作，融合乘加，跨通道数据重排等等；
AVX-512出现在2014年，由256bit拓展到512bit；

所谓SIMD，本质上就是把f32，i32，f64，i64，互相转换来转换去，算来算去的过程改为了向量化用于加速。此外MIPS，ARM都有自己的SIMD指令集，因此SIMD指令不能跨平台。

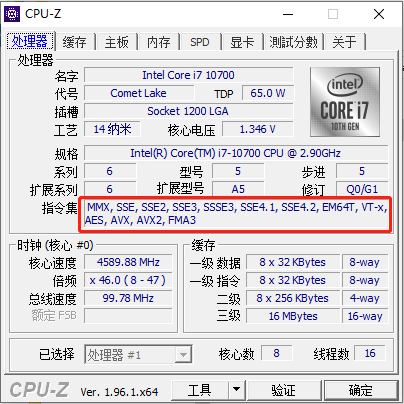
如何查看当前cpu支持的指令集

win

使用cpu-z

linux

执行 cat /proc/cpuinfo

processor       : 15
vendor_id       : AuthenticAMD
cpu family      : 25
model           : 80
model name      : AMD Ryzen 7 5825U with Radeon Graphics
stepping        : 0
microcode       : 0xa50000c
cpu MHz         : 1600.000
cache size      : 512 KB
physical id     : 0
siblings        : 16
core id         : 7
cpu cores       : 8
apicid          : 15
initial apicid  : 15
fpu             : yes
fpu_exception   : yes
cpuid level     : 16
wp              : yes
flags           : fpu vme de pse tsc msr pae mce cx8 apic sep mtrr pge mca cmov pat pse36 clflush mmx fxsr sse sse2 ht syscall nx mmxext fxsr_opt pdpe1gb rdtscp lm constant_tsc rep_good nopl nonstop_tsc cpuid extd_apicid aperfmperf rapl pni pclmulqdq monitor ssse3 fma cx16 sse4_1 sse4_2 movbe popcnt aes xsave avx f16c rdrand lahf_lm cmp_legacy svm extapic cr8_legacy abm sse4a misalignsse 3dnowprefetch osvw ibs skinit wdt tce topoext perfctr_core perfctr_nb bpext perfctr_llc mwaitx cpb cat_l3 cdp_l3 hw_pstate ssbd mba ibrs ibpb stibp vmmcall fsgsbase bmi1 avx2 smep bmi2 erms invpcid cqm rdt_a rdseed adx smap clflushopt clwb sha_ni xsaveopt xsavec xgetbv1 xsaves cqm_llc cqm_occup_llc cqm_mbm_total cqm_mbm_local clzero irperf xsaveerptr rdpru wbnoinvd cppc arat npt lbrv svm_lock nrip_save tsc_scale vmcb_clean flushbyasid decodeassists pausefilter pfthreshold avic v_vmsave_vmload vgif v_spec_ctrl umip pku ospke vaes vpclmulqdq rdpid overflow_recov succor smca fsrm
bugs            : sysret_ss_attrs spectre_v1 spectre_v2 spec_store_bypass
bogomips        : 3992.46
TLB size        : 2560 4K pages
clflush size    : 64
cache_alignment : 64
address sizes   : 48 bits physical, 48 bits virtual
power management: ts ttp tm hwpstate cpb eff_freq_ro [13] [14]

用Rust该怎么玩Simd呢？

在标准库下的core_simd中的examples中有这样的演示代码。

比如我们现在想实现两个Slice 相乘并加和，最开始我们可能会这么实现：

pub fn dot_prod_scalar_0(a: &[f32], b: &[f32]) -> f32 {
    assert_eq!(a.len(), b.len());

    a.iter().zip(b.iter()).map(|(a, b)| a * b).sum()
}

先zip合并两个Slice，再将元组的Slice转为相乘结果，再加和

pub fn dot_prod_scalar_1(a: &[f32], b: &[f32]) -> f32 {
    assert_eq!(a.len(), b.len());
    a.iter()
        .zip(b.iter())
        .fold(0.0, |a, zipped| a + zipped.0 * zipped.1)
}

使用fold再迭代时跌加，可以避免产生相乘结果的中间态，直接迭代两个Slice相乘结果。

我们再来看下怎么利用Simd加速这个功能（要执行这段代码需添加 #![feature(portable_simd)] ）：

pub fn dot_prod_simd_0(a: &[f32], b: &[f32]) -> f32 {
    assert_eq!(a.len(), b.len());
    a.array_chunks::<4>()
        .map(|&a| f32x4::from_array(a))
        .zip(b.array_chunks::<4>().map(|&b| f32x4::from_array(b)))
        .map(|(a, b)| (a * b).reduce_sum())
        .sum()
}

上面的代码将两个Slice切分为4个一组的数组，然后调用 f32x4::from_array 转为向量。然后还是zip合并两组向量，两边每组向量相乘
时将调用simd指令。然后将结果（结果还是个向量）调用reduce_sum 加和，最后再将整个Slice加和。

还能进一步优化：

pub fn dot_prod_simd_1(a: &[f32], b: &[f32]) -> f32 {
    assert_eq!(a.len(), b.len());
    // TODO handle remainder when a.len() % 4 != 0
    a.array_chunks::<4>()
        .map(|&a| f32x4::from_array(a))
        .zip(b.array_chunks::<4>().map(|&b| f32x4::from_array(b)))
        .fold(f32x4::splat(0.0), |acc, zipped| acc + zipped.0 * zipped.1)
        .reduce_sum()
}

和前面的思路类似，省去了逐对reduce_sum 再 一起sum的过程，fold过程中计算，将两边的相乘并加到全0的simd中。最后只剩下fold结果，一个simd，执行一次reduce_sum就好。

还能优化吗？可以的：

use std_float::StdFloat;
pub fn dot_prod_simd_2(a: &[f32], b: &[f32]) -> f32 {
    assert_eq!(a.len(), b.len());
    // TODO handle remainder when a.len() % 4 != 0
    let mut res = f32x4::splat(0.0);
    a.array_chunks::<4>()
        .map(|&a| f32x4::from_array(a))
        .zip(b.array_chunks::<4>().map(|&b| f32x4::from_array(b)))
        .for_each(|(a, b)| {
            res = a.mul_add(b, res);
        });
    res.reduce_sum()
}

这里引入一个新api mul_add 先将a,b 相乘，再和res叠加，将前面的fold函数在指令层面完成。

这里需要注意的是，上面的array_chucks操作遇到长度不能被4整除的Slice，剩下的尾巴不会被放到simd指令执行，比如我们尝试使用(0..13.0) 和 (0..12) 调用 dot_prod_simd_1 会得到相同的结果。

#[test]
fn t1() {
    let a = &(0..12).map(|e|e as f32).collect::<Vec<f32>>();
    let b = &(0..13).map(|e|e as f32).collect::<Vec<f32>>();
    assert_eq!(&dot_prod_simd_2(&a, &a),&dot_prod_simd_2(&b, &b));
}

这里我们处理下被忽略的尾巴：

const LANES: usize = 4;
pub fn dot_prod_simd_3(a: &[f32], b: &[f32]) -> f32 {
    assert_eq!(a.len(), b.len());

    let (a_extra, a_chunks) = a.as_rchunks();
    let (b_extra, b_chunks) = b.as_rchunks();

    // These are always true, but for emphasis:
    assert_eq!(a_chunks.len(), b_chunks.len());
    assert_eq!(a_extra.len(), b_extra.len());

    let mut sums = [0.0; LANES];
    for ((x, y), d) in std::iter::zip(a_extra, b_extra).zip(&mut sums) {
        *d = x * y;
    }

    let mut sums = f32x4::from_array(sums);
    std::iter::zip(a_chunks, b_chunks).for_each(|(x, y)| {
        sums += f32x4::from_array(*x) * f32x4::from_array(*y);
    });

    sums.reduce_sum()
}