并查集与应用

概念

并查集是一种树型的数据结构，用于处理一些不相交集合的合并及查询问题。

关键字：不相交，集合。大量数据做快速查询合并时，并查集效果最好。

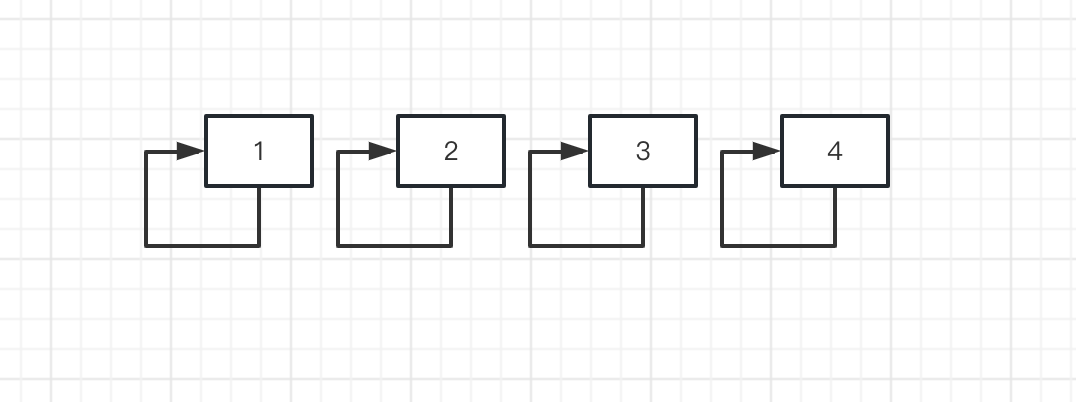
原理

构建一个数组，数组保存每个元素的父元素。初始时，每个元素的父元素都是其自身。

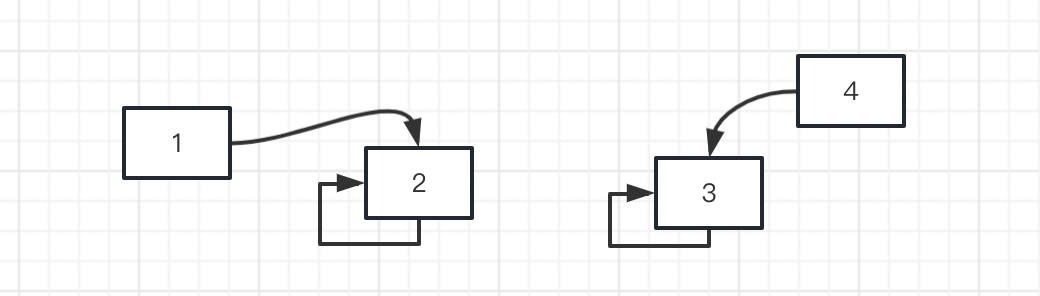
根据业务逻辑将集合分组合并，所谓合并就是将一个元素的根节点指向另一组的根节点 。

所以最终判断某个元素是否和另一个元素同组的方式就是递归地找它的父节点，直到父节点就是自身。同组的根节点一定相同。不同组的根节点一定不同。

所以假设我们需要知道节点99和节点5是否同组，只需递归地找到他们的根节点分别为102和3则可以断定99和5位于不同组。

上面的概念代码实现为:

struct UnionFind {
    par: Vec<usize>,
}

impl UnionFind {
    fn new(size: usize) -> Self {
        let mut par = vec![0; size];
        for i in 0..size {
            par[i] = i;
        }
        UnionFind { par }
    }

    fn find(&self, x: usize) -> usize {
        if self.par[x] == x {
            x
        } else {
            self.find(self.par[x])
        }
    }

    fn union(&mut self, a: usize, b: usize) {
        let a = self.find(a);
        let b = self.find(b);
        if a == b {
            return;
        }
        self.par[a] = b;
    }
}

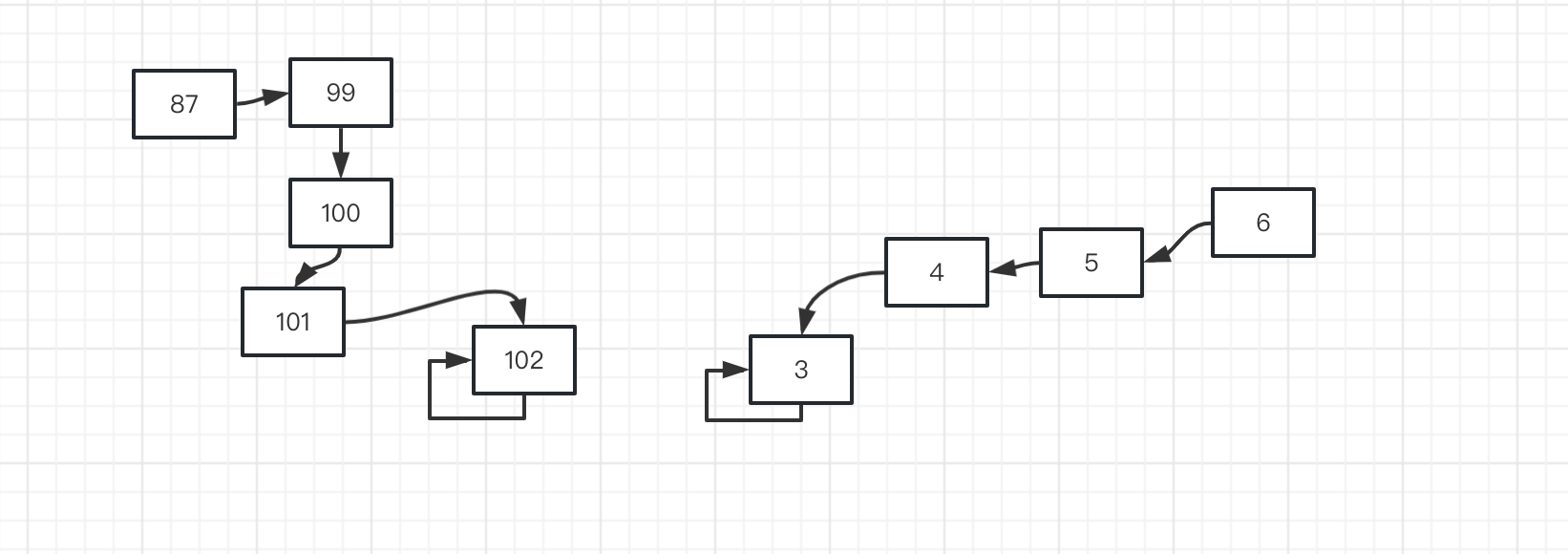
这一版实现能满足我们的基本需求，但是也存在一些问题。比如树的高度可能过高，甚至可能导致这里find退化为O(n)复杂度。

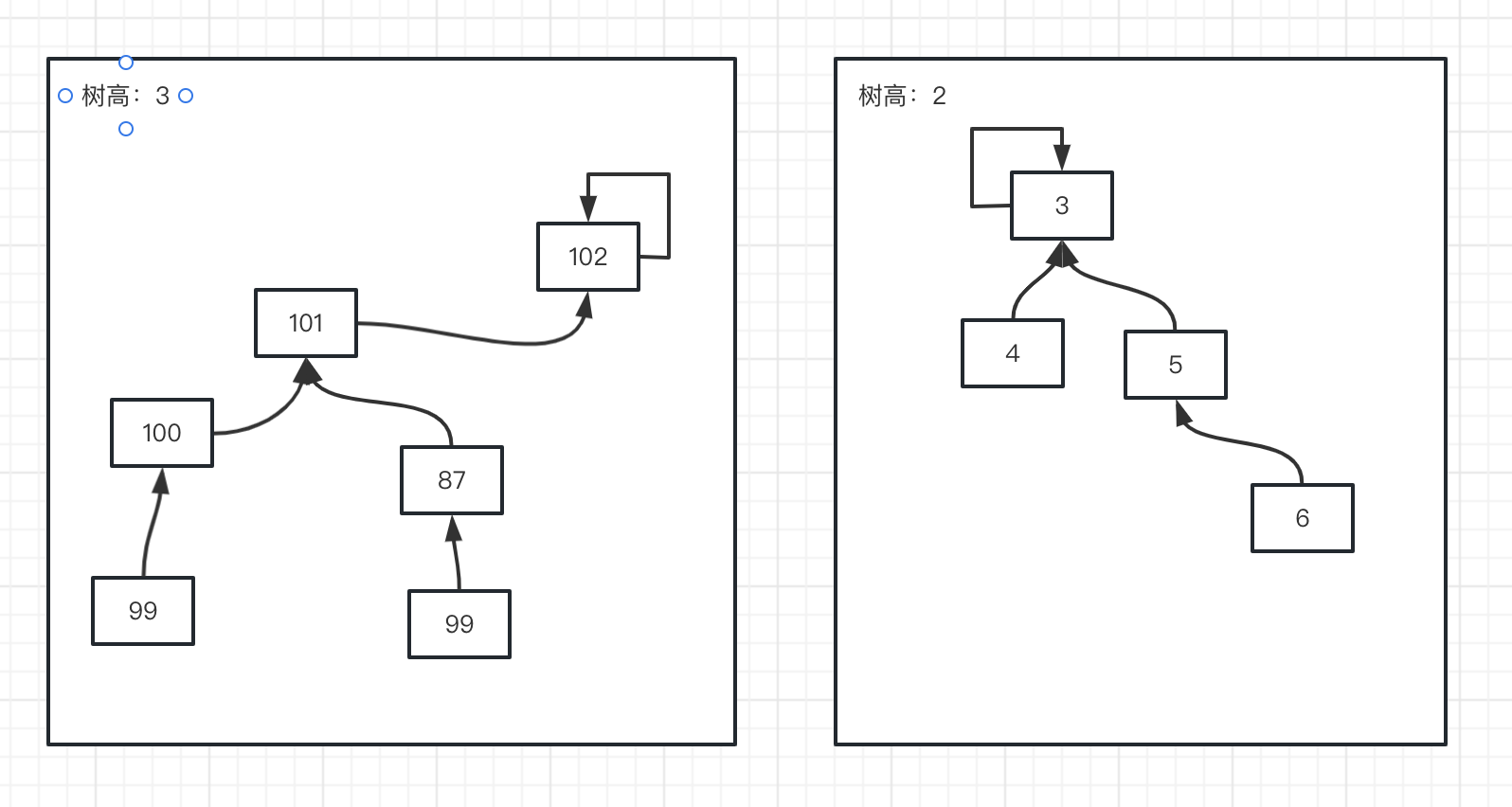
一种可行的方式是我们维护每个集合的树高。然后每次合并时将树高低的集合根节点指向树高较高的根节点。可以有效避免树高过高。

struct UnionFind {
    par: Vec<usize>,
    rank: Vec<usize>,
}

impl UnionFind {
    fn new(size: usize) -> Self {
        let mut par = vec![0; size];
        let rank = vec![0; size];
        for i in 0..size {
            par[i] = i;
        }
        Self { par, rank }
    }

    fn find(&self, x: usize) -> usize {
        if self.par[x] == x {
            x
        } else {
            self.find(self.par[x])
        }
    }

    fn union(&mut self, a: usize, b: usize) {
        let a = self.find(a);
        let b = self.find(b);
        if a == b {
            return;
        }
        if self.rank[a] < self.rank[b] {
            self.par[a] = b;
        } else {
            self.par[b] = a;
            if self.rank[a] == self.rank[b] {
                self.rank[a] += 1;
            }
        }
    }
}

此外，我们希望并查集的树越扁平越好，理想状态下是一个大二层结构：一个根节点下包含所有子节点。所以这里每次查找的时候可以有一个路径压缩的优化，每次查找到自己节点的根节点后，将自己的父节点置为根节点。避免路径上的搜素，提升后续效率。

这里find就需要改为mut了

fn find(&mut self, x: usize) -> usize {
    if self.par[x] == x {
        return x;
    }
    self.par[x] = self.find(self.par[x]);
    self.par[x]
}

应用

leetCode 261 以图判树

给定编号从 0 到 n - 1 的 n 个结点。给定一个整数 n 和一个 edges 列表，其中 edges[i] = [ai, bi] 表示图中节点 ai 和 bi 之间存在一条无向边。

如果这些边能够形成一个合法有效的树结构，则返回 true ，否则返回 false 。

分析

由于数据量比较小，这里也不整各种优化了。我们需要构建并查集，遍历edges填入并查集，如果已经存在两个节点根节点相同，说明必然存在环。

class Solution {
    public boolean validTree(int n, int[][] edges) {
        int[] p = new int[n];
       for(int i=0;i<p.length;i++)p[i]=i;
       for(int[] edge:edges) {
           int x0 = find(edge[0],p);
           int x1 = find(edge[1],p);
           if(x1!=x0)p[x0] = p[x1];
           // 如果x0=x1说明有环
           else return false;
       }

        int count = 0;
        for(int i=0;i<p.length;i++)if(p[i]==i) count++;
        // 如果不为1说么要么有环，要么有独立节点（连通分量）
        return count==1;
    }

    int find(int x,int[] p) {
        if(x==p[x])return x;
        else return find(p[x],p);
    }
}